Contents

Ejercicio 1

x=[10;20;40;60;80];
y=[x,log(x)];

fprintf('\n Numero Natural \t log\n')
fprintf('\t%4i\t\t%8.5f\n',y')


 Numero Natural 	 log
	  10		 2.30259
	  20		 2.99573
	  40		 3.68888
	  60		 4.09434
	  80		 4.38203
	 100		 4.60517

Ejercicio 5

%$$U^{-1}L^{-1}B$$
%Calculamos la matriz incógnita:
A=[100 0 0 0 -1 1 0;0 200 0 0 0 -1 1;0 0 50 0 -1 0 0;0 0 0 100 0 -1 0;0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0];
b=[0 0 -50 -50 -50 25 0]';
X=A\b

X =

   1.0e+03 *

    0.0054
    0.0009
    0.0196
    0.0045
    1.0321
    0.4964
    0.3179

Ejercicio 6

%$$U^{-1}L^{-1}B$$
%Aplicamos la factorización:
A=[100 0 0 0 -1 1 0;0 200 0 0 0 -1 1;0 0 50 0 -1 0 0;0 0 0 100 0 -1 0;0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0];
b=[0 0 -50 -50 -50 25 0]';
[L U]=lu(A)
C=L*U
%Resolvemos el sistema:
X=inv(U)*inv(L)*b

L =

    1.0000         0         0         0         0         0         0
         0    0.6667         0         0         0    1.0000         0
         0         0    1.0000         0         0         0         0
         0         0         0    1.0000         0         0         0
         0    1.0000         0         0         0         0         0
    0.0100         0    0.0200         0    1.0000         0         0
    0.0100   -0.0033         0   -0.0100    0.3333    0.0167    1.0000


U =

  100.0000         0         0         0   -1.0000    1.0000         0
         0  300.0000         0         0         0         0   -1.0000
         0         0   50.0000         0   -1.0000         0         0
         0         0         0  100.0000         0   -1.0000         0
         0         0         0         0    0.0300   -0.0100         0
         0         0         0         0         0   -1.0000    1.6667
         0         0         0         0         0         0   -0.0311


C =

  100.0000         0         0         0   -1.0000    1.0000         0
         0  200.0000         0         0         0   -1.0000    1.0000
         0         0   50.0000         0   -1.0000         0         0
         0         0         0  100.0000         0   -1.0000         0
         0  300.0000         0         0         0         0   -1.0000
    1.0000         0    1.0000         0         0         0         0
    1.0000   -1.0000         0   -1.0000    0.0000         0         0

X =

   1.0e+03 *

    0.0054
    0.0009
    0.0196
    0.0045
    1.0321
    0.4964
    0.3179

Ejercicio 7

A=[0 1 -1;-6 -11 6;-6 -11 5];
[X,D]=eig(A);
fprintf('\n Autovectores (Columnas de la matriz)\n')
X(:,1)
fprintf('\n Autovalores (Diagonal)\n')
D

 Autovectores (Columnas de la matriz)

ans =

    0.7071
    0.0000
    0.7071


 Autovalores (Diagonal)

D =

   -1.0000         0         0
         0   -2.0000         0
         0         0   -3.0000

Ejercicio 8

Y=[1.5-2j -.35+1.2j;-.35+1.2j 0.9-1.6j];
I=[30+40j;20+15j]
V=Y\I
S=V.*conj(I)

I =

  30.0000 +40.0000i
  20.0000 +15.0000i


V =

   3.5902 +35.0928i
   6.0155 +36.2212i


S =

   1.0e+03 *

   1.5114 + 0.9092i
   0.6636 + 0.6342i

Ejercicio 11

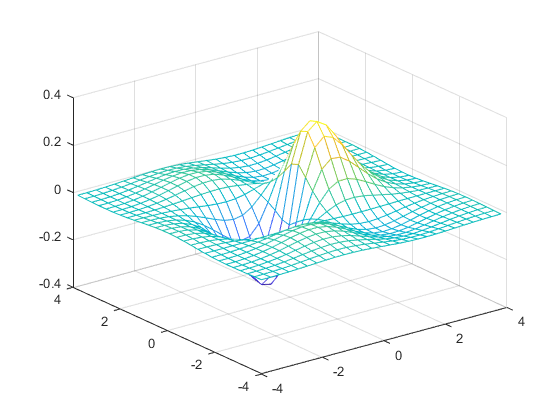
[x,y]=meshgrid(-4:0.3:4);
z=sin(x).*cos(y).*exp(-(x.^2+y.^2).^0.5);
mesh(x,y,z)

Ejercicio 12

% function y = HalfSine(t, y, z)
% h = sin(pi*t/5).*(t<=5);
% y = [y(2); -2*z*y(2)-y(1)+h];
[t, yy] = ode45(@HalfSine, [0 35], [1 0], [ ], 0.15);
plot(t, yy(:,1))

Ejercicio 13

k = 5; m = 10; fo = 10;Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N; df = (0:N/2-1)/T;

g1 = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
An1 = abs(fft(g1, N))/N;
plot(df, 2*An1(1:N/2))

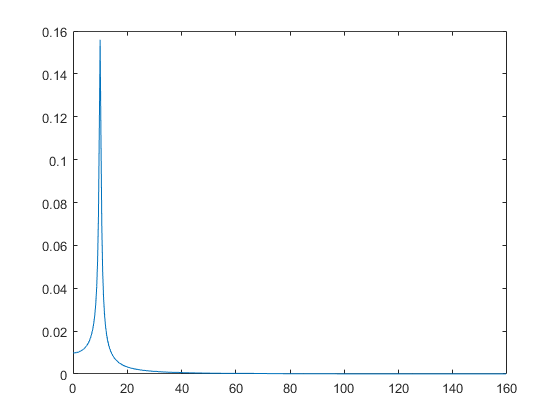
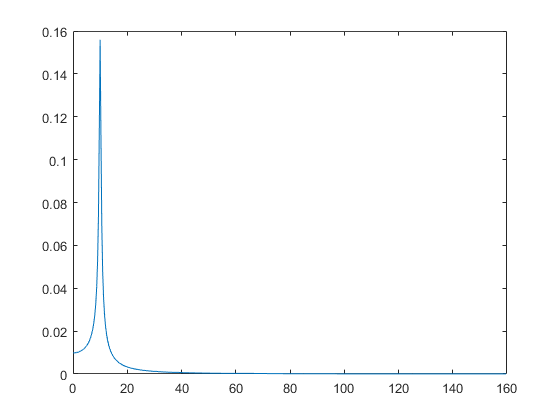
g2 = exp(-2*ts).*sin(2*pi*fo*ts);
An2 = abs(fft(g2, N))/N;
plot(df, 2*An2(1:N/2))

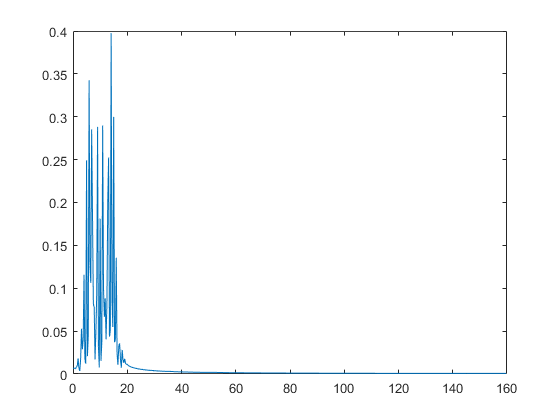
g3 = sin(2*pi*fo*ts+5*sin(2*pi*(fo/10)*ts));
An3 = abs(fft(g3, N))/N;
plot(df, 2*An3(1:N/2))

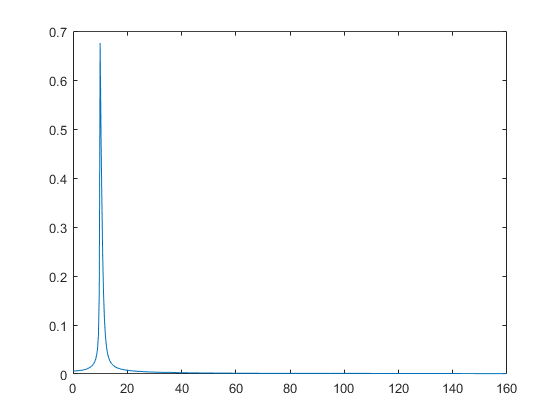
g4 = sin(2*pi*fo*ts-5*exp(-2*ts));
An4 = abs(fft(g4, N))/N;
plot(df, 2*An4(1:N/2))

Ejercicio 14

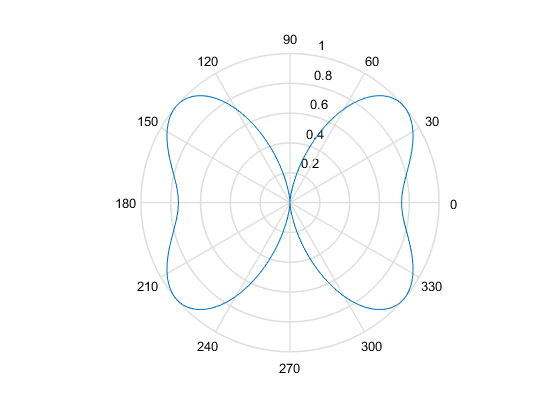
theta = linspace(-pi, pi, 300);
p = abs(besselj(2, -4*cos(theta)));
polar(theta, p/max(p))